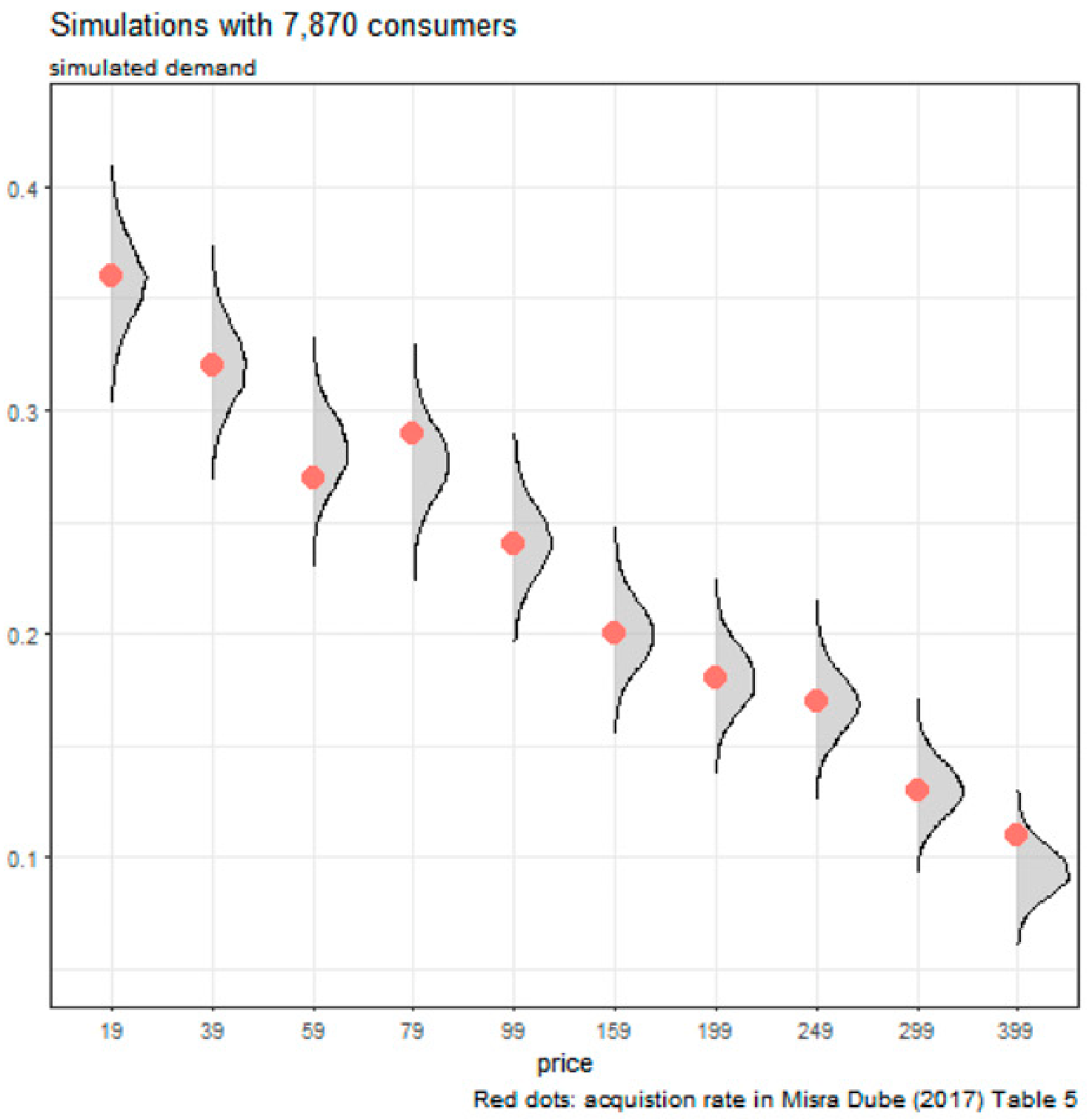
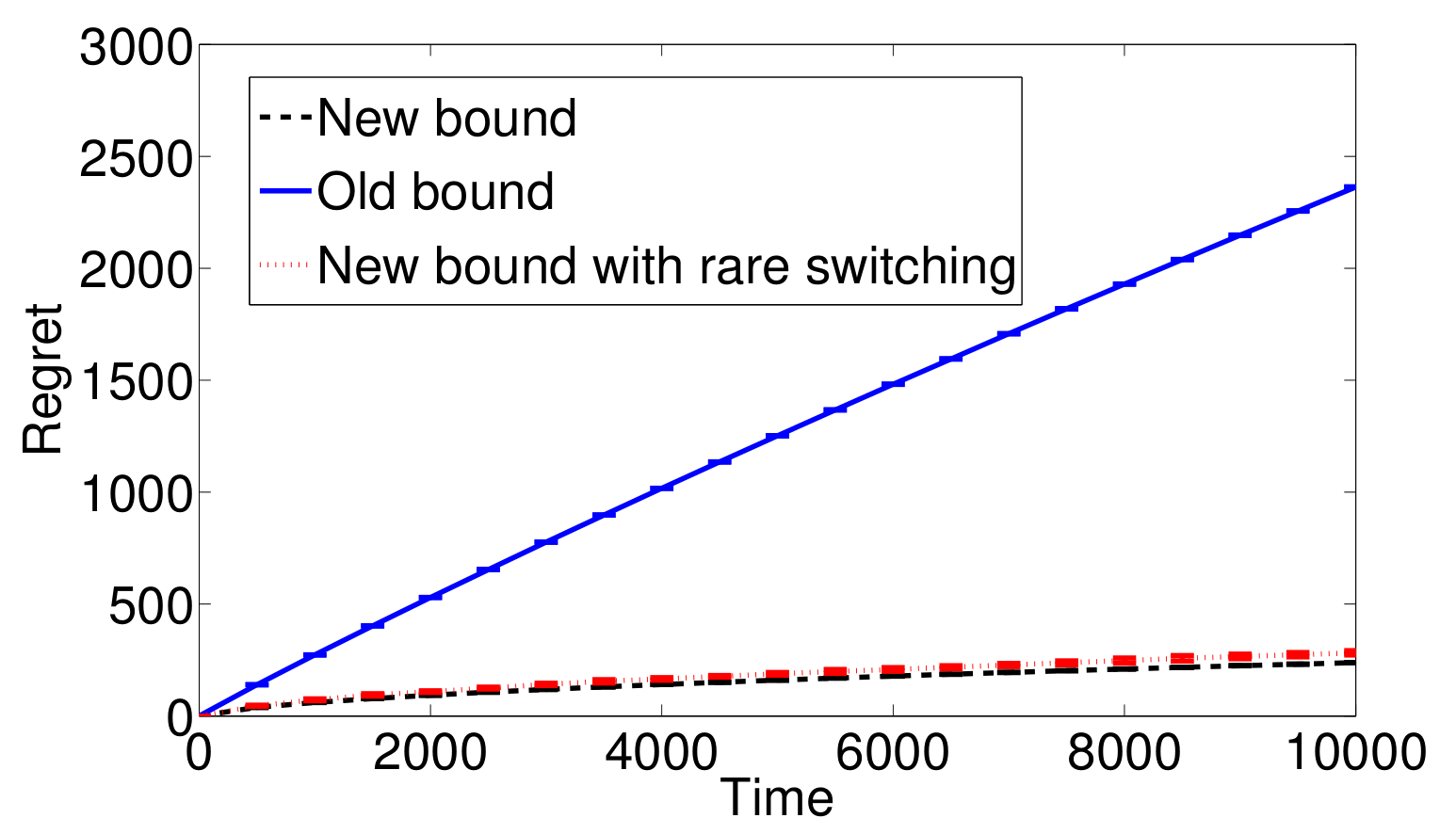
Improvements in UCB-PI-untuned:
- assign an action a zero value if the upper bound of potential returns is lower than the highest lower bound across all actions. Economically, we do not explore dominated options (the optimal return is still lower than the other lower returns).
- scale the exploration bonus by price since the original reward in UCB1 is but now for dummy demand.
Improvements in UCB-PI-tuned: add an additional tuning factor : size of uncertainty ↑ exploration bonus↑