For partial identified , where:
That means for a given price, the weighted average of probability that each segment can accept/reject the price for sure.
Given consumer’s response, their potential preference types are bounded.
Preference: θs∈{θ1,θ2,...θK}, where θk>pk and θk<pk+1
Three cases:
Estimation of price range pmin and pmax:
Note: do not use information of 3
For a consumer with preference range [$2,$4] (Seg A accept and Seg B reject for sure, and same group size), then the probability of accepting pk=3 is specified as 0.5=1∗0.5+0∗0.5. They did not use 20% accept ratio in for Seg A when price is $3.
For partial identified Ht[π(pk)]=[LBt(π(pk)),UBt(π(pk))], where:
That means for a given price, the weighted average of probability that each segment can accept/reject the price for sure.
This paper provides an elegant solution to solve exploration-exploitation tradeoff in a "cold-start" pricing problem.
Utility function:
ui=vi−p
We assume heterogeneity among consumers can be separated as observable (by descriptive variables Zi) and unobservable heterogeneity.
vi=f(Zi)+νi.
Segments: the firm assign consumers into segments S, and s∈S represents combination of descriptive variables Zi.
vi=vs+νi,νi∈[−δ,δ]
A monopolist determines the price with information that the consumer valuation is [vL,vH]
Profits: The firm can determine the price from price set p∈{p1,p2,...pk} and face with demand D(p), thus the profit is π(p)=pD(p).
Price experimentation: Suppose by time t, the firm has charged pk a total of nkt times. Let πk,1,πk,2,…,πk,nkt be realizations of profit per consumer from every time that price pk has been charged.
Pricing problem:
pt=Ψ({pτ,πτ∣τ=1,…,t−1})
Regret(Ψ,{π(pk)},t)=E[τ=1∑tπ∗−πpτ]=τ=1∑t(π∗−π(pτ))=π∗t−k=1∑Kπ(pk)E[nkt]
UCB algorithm is the sum of "expected reward" and an "exploration bonus".
UCB1kt=πˉkt+nkt2logt
Here the bonus term can be written as nktαlogt when α=2, and the paper proposed another value to achieve better performance.
Repeat-purchase data can help to backout consumer preference.
For example:
then her preference lies between $3 and $6.
However, this case is overly restrictive, thus the paper focus on cross-sectional learning across consumers.
Given consumer’s response, their potential preference types are bounded.
Preference: θs∈{θ1,θ2,...θK}, where θk>pk and θk<pk+1
Three cases:
Estimation of price range pmin and pmax:
Note: do not use information of 3
For a consumer with preference range [$2,$4] (Seg A accept and Seg B reject for sure, and same group size), then the probability of accepting pk=3 is specified as 0.5=1∗0.5+0∗0.5. They did not use 20% accept ratio in for Seg A when price is $3.
For partial identified Ht[π(pk)]=[LBt(π(pk)),UBt(π(pk))], where:
That means for a given price, the weighted average of probability that each segment can accept/reject the price for sure.
UCB1ktUCB-tunedkt=πˉkt+nkt2logt=πˉkt+nktlogtmin(41,Vkt)
Next step:
UCB-PI-untunedktUCB-PI-tunedkt={πˉkt+pknkt2logt0 if UBt(π(pk))>maxlLBt(π(pl)), if UBt(π(pk))≤maxlLBt(π(pl)).={πˉkt+02pkδ^nktlogtmin(41, Vkt) if UBt(π(pk))≤lmaxLBt(π(pl)). if UBt(π(pk))>lmaxLBt(π(pl)),
Improvements in UCB-PI-untuned:
Improvements in UCB-PI-tuned: add an additional tuning factor 2δ^: size of uncertainty ↑ exploration bonus↑
Questions I have while reading the paper:
Questions I found while reading related papers:
Difficult to scale efficiently with high-dimensional characteristics
Stronger UCB variants
Questions when I connected the paper with reality:
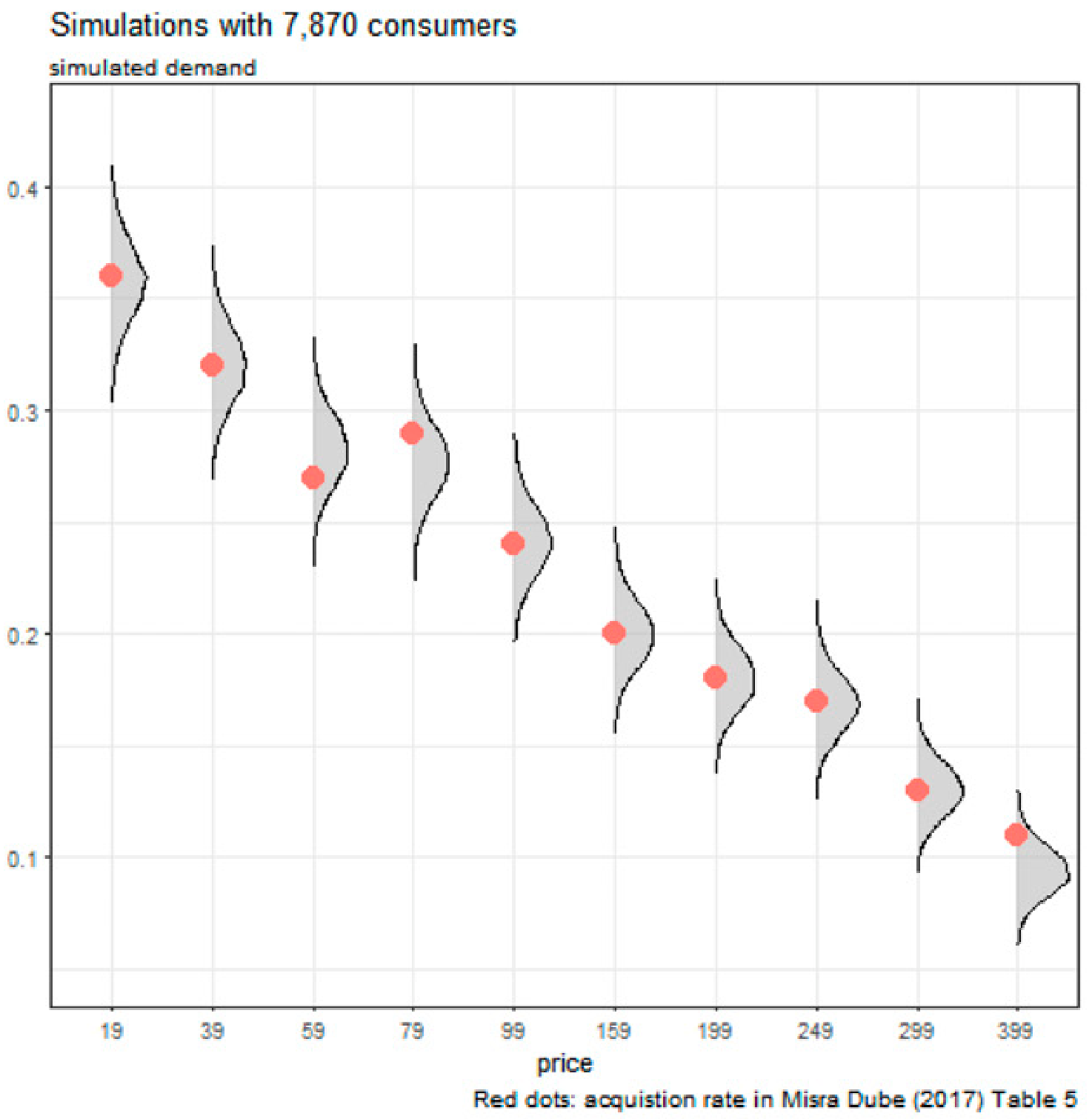
When the price is 79, the demand shift upward.
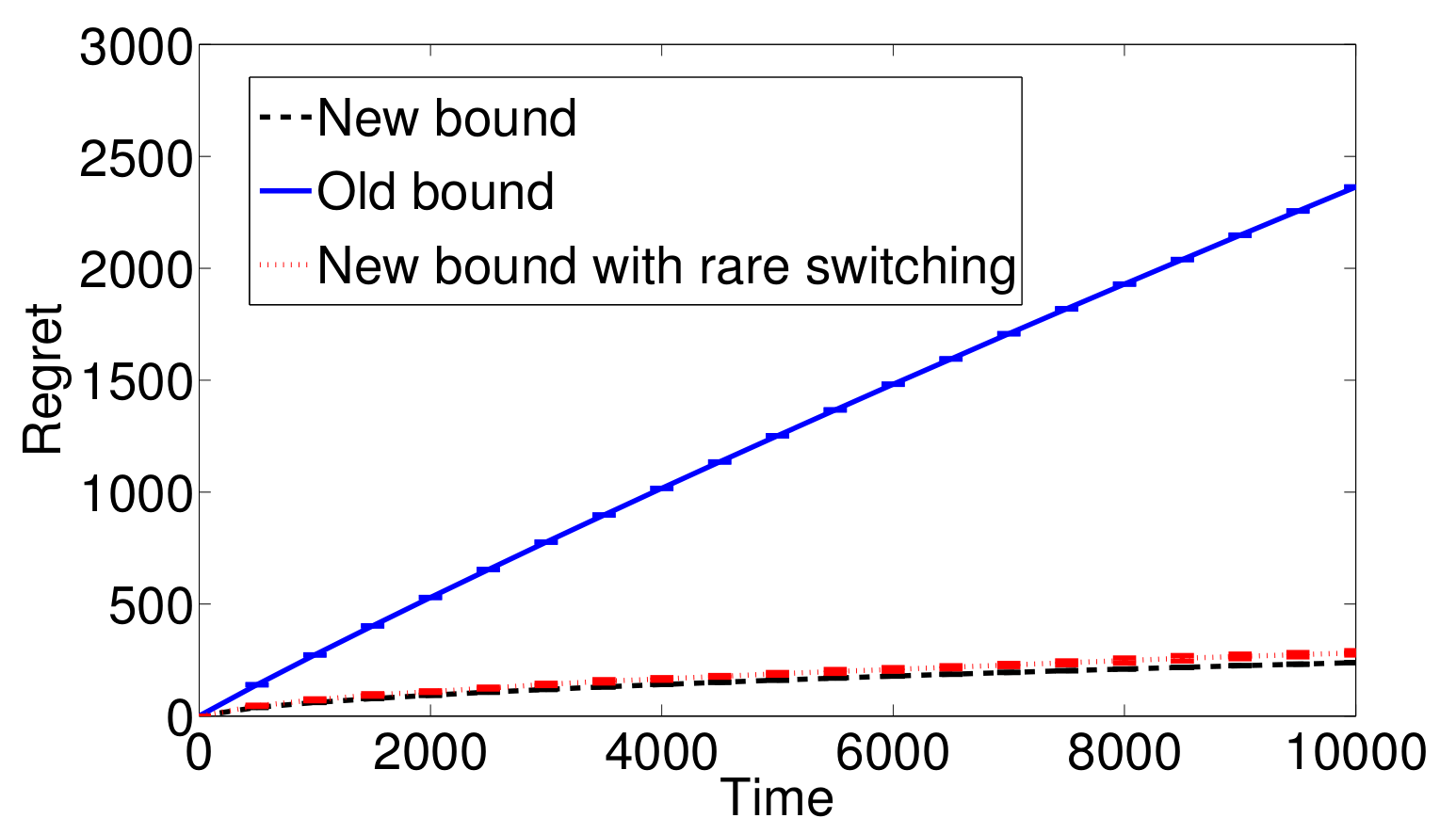
The modifed UCB has much better performance.
In this Big Data era, a "global optimal pricing strategy" is hard to find.
Lets say we wanna train a strategy for Amazon, we will find following problems:
Research Question: how to optimize the decentralized learning process using the same trick in Misra paper?

Utility, preference, price settings. follow Misra paper.
For the communication problem, I followed Shi and Shen (2021).
Non-iid data generation. Data in local servers 1,2,...l correlated with "whole data", but are non-iid. For segment s, assume the true mean is μs, and the local mean follows μs,l where:
μs,i=μs,j,i=j.
Communication Loss. Every time a central server communicate with local server to update the model and send back the model to each local server, it incurs constant cost C.
Shi and Shen (2021) developed Fed2-UCB algorithms to solve the Federated learning based on a stylized demand distritbution (normal distribution family), which might not apply to a distribution-free situation (Misra paper)
we are considering this question: whether the optimal global pricing strategy is the combination of local optimal solutions?